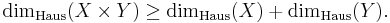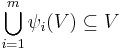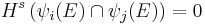Hausdorff dimension

In mathematics, the Hausdorff dimension (also known as the Hausdorff–Besicovitch dimension) is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space. That is, the Hausdorff dimension of an n-dimensional inner product space equals n. This means, for example, the Hausdorff dimension of a point is zero, the Hausdorff dimension of a line is one, and the Hausdorff dimension of the plane is two. There are, however, many irregular sets that have noninteger Hausdorff dimension. The concept was introduced in 1918 by the mathematician Felix Hausdorff. Many of the technical developments used to compute the Hausdorff dimension for highly irregular sets were obtained by Abram Samoilovitch Besicovitch.

1 Informal discussion
2 Formal definition
3 Examples
4 Properties of Hausdorff dimension
5 Self-similar sets
6 The Hausdorff dimension Theorem
7 See also
8 Historical references
9 Notes
10 References

Informal discussion

The intuitive dimension of a geometric object is the number of independent parameters you need to pick out a unique point inside. But you can easily take a single real number, one parameter, and split its digits to make two real numbers. The example of a space-filling curve shows that you can even take one real number into two continuously, so that a one-dimensional object can completely fill up a higher dimensional object.

Every space filling curve hits every point many times, and does not have a continuous inverse. It is impossible to map two dimensions onto one in a way that is continuous and continuously invertible. The topological dimension explains why. The Lebesgue covering dimension is defined as the minimum number of overlaps that small open balls need to have in order to completely cover the object. When you try to cover a line by dropping intervals on it, you always end up covering some points twice. Covering a plane with disks, you end up covering some points three times, etc. The topological dimension tells you how many different little balls connect a given point to other points in the space, generically. It tells you how difficult it is to break a geometric object apart into pieces by removing slices.

But the topological dimension doesn't tell you anything about volumes. A curve which is almost space filling can still have topological dimension one, even if it fills up most of the area of a region. A fractal has an integer topological dimension, but in terms of the amount of space it takes up, it behaves as a higher dimensional space. The Hausdorff dimension defines the size notion of dimension, which requires a notion of radius, or metric.

Consider the number N(r) of balls of radius at most r required to cover X completely. When r is small, N(r) is large. If N(r) always grows as 1/r^d as r approaches zero, then X has Hausdorff dimension d. The precise definition requires that the dimension "d" so defined is a critical boundary between growth rates that are insufficient to cover the space, and growth rates which are overabundant.

For shapes which are smooth, or shapes with a small number of corners, the shapes of traditional geometry and science, the Hausdorff dimension is an integer. But Benoît Mandelbrot observed that fractals, sets with noninteger Hausdorff dimensions, are found everywhere in nature. He observed that the proper idealization of most rough shapes you see around you is not in terms of smooth idealized shapes, but in terms of fractal idealized shapes:

clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line. ^[1]

The Hausdorff dimension is a successor to the less sophisticated but in practice very similar box-counting dimension or Minkowski-Bouligand dimension. This counts the squares of graph paper in which a point of X can be found as the size of the squares is made smaller and smaller. For fractals which occur in nature, the two notions coincide. The packing dimension is yet another similar notion. These notions (packing dimension, Hausdorff dimension, Minkowski-Bouligand dimension) all give the same value for many shapes, but there are well documented exceptions.

Formal definition

Let $X$ be a metric space. If $S\subset X$ and $d\in[0,\infty)$ , the $d$ -dimensional Hausdorff content of $S$ is defined by

$C_H^d(S):=\inf\Bigl\{\sum_i r_i^d:\text{ there is a cover of } S\text{ by balls with radii }r_i>0\Bigr\}.$

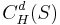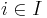In other words, $C_H^d(S)$ is the infimum of the set of numbers $\delta\ge 0$ such that there is some (indexed) collection of balls $\{B(x_i,r_i):i\in I\}$ covering $S$ with $r_i>0$ for each $i\in I$ which satisfies $\sum_{i\in I}r_i^d<\delta$ . (Here, we use the standard convention that inf Ø =∞.) The Hausdorff dimension of $X$ is defined by

$\operatorname{dim}_{\operatorname{H}}(X):=\inf\{d\ge 0: C_H^d(X)=0\}.$

Equivalently, 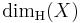$\operatorname{dim}_{\operatorname{H}}(X)$ may be defined as the infimum of the set of $d\in[0,\infty)$ such that the $d$ -dimensional Hausdorff measure of $X$ is zero. This is the same as the supremum of the set of $d\in[0,\infty)$ such that the $d$ -dimensional Hausdorff measure of $X$ is infinite (except that when this latter set of numbers $d$ is empty the Hausdorff dimension is zero).

Examples

The Euclidean space 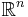$\mathbb{R}^{n}$ has Hausdorff dimension n.
The circle S¹ has Hausdorff dimension 1.
Countable sets have Hausdorff dimension 0.
Fractals often are spaces whose Hausdorff dimension strictly exceeds the topological dimension. For example, the Cantor set (a zero-dimensional topological space) is a union of two copies of itself, each copy shrunk by a factor 1/3; this fact can be used to prove that its Hausdorff dimension is $\ln 2/\ln 3,$ which is approximately $0{.}63$ The Sierpinski triangle is a union of three copies of itself, each copy shrunk by a factor of 1/2; this yields a Hausdorff dimension of $\ln 3/ \ln 2$ , which is approximately $1{.}58$ .
Space-filling curves like the Peano and the Sierpiński curve have the same Hausdorff dimension as the space they fill.
The trajectory of Brownian motion in dimension 2 and above has Hausdorff dimension 2 almost surely.
An early paper by Benoit Mandelbrot entitled How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension and subsequent work by other authors have claimed that the Hausdorff dimension of many coastlines can be estimated. Their results have varied from 1.02 for the coastline of South Africa to 1.25 for the west coast of Great Britain. However, 'fractal dimensions' of coastlines and many other natural phenomena are largely heuristic and cannot be regarded rigorously as a Hausdorff dimension. It is based on scaling properties of coastlines at a large range of scales; however, it does not include all arbitrarily small scales, where measurements would depend on atomic and sub-atomic structures, and are not well defined.
The bond system of an amorphous solid changes its Hausdorff dimension from Euclidian 3 below glass transition temperature T_g (where the amorphous material is solid), to fractal 2.55±0.05 above T_g, where the amorphous material is liquid.^[2]

Properties of Hausdorff dimension

Hausdorff dimension and inductive dimension

Let X be an arbitrary separable metric space. There is a topological notion of inductive dimension for X which is defined recursively. It is always an integer (or +∞) and is denoted dim_ind(X).

Theorem. Suppose X is non-empty. Then

$\operatorname{dim}_{\mathrm{Haus}}(X) \geq \operatorname{dim}_{\mathrm{ind}}(X).$

Moreover

$\inf_Y \operatorname{dim}_{\mathrm{Haus}}(Y) =\operatorname{dim}_{\mathrm{ind}}(X)$

where Y ranges over metric spaces homeomorphic to X. In other words, X and Y have the same underlying set of points and the metric d_Y of Y is topologically equivalent to d_X.

These results were originally established by Edward Szpilrajn (1907–1976). The treatment in Chapter VII of the Hurewicz and Wallman reference is particularly recommended.

Hausdorff dimension and Minkowski dimension

The Minkowski dimension is similar to the Hausdorff dimension, except that it is not associated with a measure. The Minkowski dimension of a set is at least as large as the Hausdorff dimension. In many situations, they are equal. However, the set of rational points in $[0,1]$ has Hausdorff dimension zero and Minkowski dimension one. There are also compact sets for which the Minkowski dimension is strictly larger than the Hausdorff dimension.

Hausdorff dimensions and Frostman measures

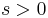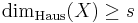If there is a measure $\mu$ defined on Borel subsets of a metric space $X$ such that $\mu(X)>0$ and $\mu(B(x,r))\le r^s$ holds for some constant $s>0$ and for every ball $B(x,r)$ in $X$ , then $\operatorname{dim}_{\mathrm{Haus}}(X) \geq s$ . A partial converse is provided by Frostman's lemma. That article also discusses another useful characterization of the Hausdorff dimension.

Behaviour under unions and products

If $X=\bigcup_{i\in I}X_i$ is a finite or countable union, then

$\operatorname{dim}_{\mathrm{Haus}}(X) =\sup_{i\in I} \operatorname{dim}_{\mathrm{Haus}}(X_i).$

This can be verified directly from the definition.

If $X$ and $Y$ are metric spaces, then the Hausdorff dimension of their product satisfies^[3]

$\operatorname{dim}_{\mathrm{Haus}}(X\times Y)\ge \operatorname{dim}_{\mathrm{Haus}}(X)%2B \operatorname{dim}_{\mathrm{Haus}}(Y).$

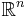This inequality can be strict. It is possible to find two sets of dimension 0 whose product has dimension 1.^[4] In the opposite direction, it is known that when $X$ and $Y$ are Borel subsets of $\R^n$ , the Hausdorff dimension of 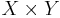$X\times Y$ is bounded from above by the Hausdorff dimension of $X$ plus the upper packing dimension of $Y$ . These facts are discussed in Mattila (1995).

Self-similar sets

Many sets defined by a self-similarity condition have dimensions which can be determined explicitly. Roughly, a set E is self-similar if it is the fixed point of a set-valued transformation ψ, that is ψ(E) = E, although the exact definition is given below.

Theorem. Suppose

$\psi_i: \mathbb{R}^n \rightarrow \mathbb{R}^n, \quad i=1, \ldots , m$

are contractive mappings on Rⁿ with contraction constant r_j < 1. Then there is a unique non-empty compact set A such that

$A = \bigcup_{i=1}^m \psi_i (A).$

The theorem follows from Stefan Banach's contractive mapping fixed point theorem applied to the complete metric space of non-empty compact subsets of Rⁿ with the Hausdorff distance.^[5]

To determine the dimension of the self-similar set A (in certain cases), we need a technical condition called the open set condition on the sequence of contractions ψ_i which is stated as follows: There is a relatively compact open set V such that

$\bigcup_{i=1}^m\psi_i (V) \subseteq V$

where the sets in union on the left are pairwise disjoint.

Theorem. Suppose the open set condition holds and each ψ_i is a similitude, that is a composition of an isometry and a dilation around some point. Then the unique fixed point of ψ is a set whose Hausdorff dimension is s where s is the unique solution of ^[6]

$\sum_{i=1}^m r_i^s = 1.$

Note that the contraction coefficient of a similitude is the magnitude of the dilation.

We can use this theorem to compute the Hausdorff dimension of the Sierpinski triangle (or sometimes called Sierpinski gasket). Consider three non-collinear points a₁, a₂, a₃ in the plane R² and let ψ_i be the dilation of ratio 1/2 around a_i. The unique non-empty fixed point of the corresponding mapping ψ is a Sierpinski gasket and the dimension s is the unique solution of

$\left(\frac{1}{2}\right)^s%2B\left(\frac{1}{2}\right)^s%2B\left(\frac{1}{2}\right)^s = 3 \left(\frac{1}{2}\right)^s =1.$

Taking natural logarithms of both sides of the above equation, we can solve for s, that is:

$s = \frac{\ln 3}{\ln 2}.$

The Sierpinski gasket is self-similar. In general a set E which is a fixed point of a mapping

$A \mapsto \psi(A) = \bigcup_{i=1}^m \psi_i(A)$

is self-similar if and only if the intersections

$H^s\left(\psi_i(E) \cap \psi_j(E)\right) =0$

where s is the Hausdorff dimension of E and $H^s$ denotes Hausdorff measure. This is clear in the case of the Sierpinski gasket (the intersections are just points), but is also true more generally:

Theorem. Under the same conditions as the previous theorem, the unique fixed point of ψ is self-similar.

The Hausdorff dimension Theorem

The following theorem deals with existence of fractals with given Hausdorff dimension in Euclidean spaces ^[7]:

Theorem. For any real 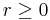$r \ge 0$ and integer $n \ge r$ , there is a continuum fractals with Hausdorff dimension $r$ in $n$ -dimensional Euclidean space.

Historical references

A. S. Besicovitch (1929). "On Linear Sets of Points of Fractional Dimensions". Mathematische Annalen 101 (1): 161–193. doi:10.1007/BF01454831.
A. S. Besicovitch; H. D. Ursell (1937). "Sets of Fractional Dimensions". Journal of the London Mathematical Society 12 (1): 18–25. doi:10.1112/jlms/s1-12.45.18.
Several selections from this volume are reprinted in Edgar, Gerald A. (1993). Classics on fractals. Boston: Addison-Wesley. ISBN 0-201-58701-7. See chapters 9,10,11
F. Hausdorff (March 1919). "Dimension und äußeres Maß". Mathematische Annalen 79 (1–2): 157–179. doi:10.1007/BF01457179.

Notes

^ Mandelbrot, Benoît (1982). The Fractal Geometry of Nature. Lecture notes in mathematics 1358. W. H. Freeman. ISBN 0716711869.
^ M.I. Ojovan, W.E. Lee. (2006). "Topologically disordered systems at the glass transition". J. Phys.: Condensed Matter 18 (50): 11507–20. Bibcode 2006JPCM...1811507O. doi:10.1088/0953-8984/18/50/007. http://eprints.whiterose.ac.uk/1958/.
^ Marstrand, J. M. (1954). "The dimension of Cartesian product sets". Proc. Cambridge Philos. Soc. 50 (3): 198–202. doi:10.1017/S0305004100029236.
^ Falconer, Kenneth J. (2003). Fractal geometry. Mathematical foundations and applications. John Wiley & Sons, Inc., Hoboken, New Jersey.
^ Falconer, K. J. (1985). "Theorem 8.3". The Geometry of Fractal Sets. Cambridge, UK: Cambridge University Press. ISBN 0-521-25694-1.
^ Tsang, K. Y. (1986). "Dimensionality of Strange Attractors Determined Analytically". Phys. Rev. Lett. 57 (12): 1390–1393. doi:10.1103/PhysRevLett.57.1390. PMID 10033437. http://prl.aps.org/abstract/PRL/v57/i12/p1390_1.
^ Soltanifar, M.(2006) On A Sequence of Cantor Fractals, Rose Hulman Undergraduate Mathematics Journal, Vol 7, No 1, paper 9.

References

Dodson, M. Maurice; Kristensen, Simon (June 12, 2003). "Hausdorff Dimension and Diophantine Approximation". Fractal geometry and applications: a jubilee of Beno\^it Mandelbrot. Part , --347, Proc. Sympos. Pure Math., 72, Part , Amer. Math. Soc., Providence, RI, . 1 (305). arXiv:math/0305399.
Hurewicz, Witold; Wallman, Henry (1948). Dimension Theory. Princeton University Press.
E. Szpilrajn (1937). "La dimension et la mesure". Fundamenta Mathematica 28: 81–9.
Marstrand, J. M. (1954). "The dimension of cartesian product sets". Proc. Cambridge Philos. Soc. 50 (3): 198–202. doi:10.1017/S0305004100029236.
Mattila, Pertti (1995). Geometry of sets and measures in Euclidean spaces. Cambridge University Press. ISBN 978-0-521-65595-8.